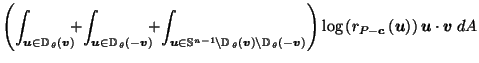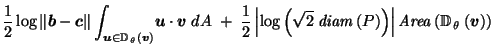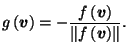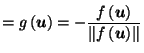A Canonical Reciprocation Center
For Convex Objects
Don Hatch
hatch@plunk.org
Date: (draft)
Last modified:
Wed Jun 4 21:36:24 PDT 2003
Abstract:
Two polyhedra 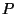 and
and 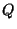 are said to be duals of each other
if there is a 1-to-1 incidence-preserving correspondence
between the (faces, edges, vertices) of
are said to be duals of each other
if there is a 1-to-1 incidence-preserving correspondence
between the (faces, edges, vertices) of 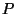 and the (vertices, edges, faces) of
and the (vertices, edges, faces) of 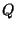 , respectively.
, respectively.
When examining the structure of a polyhedron,
it is often useful to examine its dual polyhedron
at the same time.
For example, the computer program Stella [XXX ref]
allows viewing and manipulating a (``primal'') polyhedron 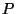 and its dual polyhedron
and its dual polyhedron 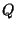 ,
either side-by-side, or superimposed.
,
either side-by-side, or superimposed.
However, the dual polyhedron 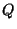 , being defined only by its structure
(i.e. incidences among its boundary elements) in relation to
, being defined only by its structure
(i.e. incidences among its boundary elements) in relation to 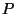 ,
is not geometrically unique: for example, starting with
any particular dual
,
is not geometrically unique: for example, starting with
any particular dual 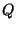 of
of 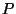 ,
any affine squashing, stretching, or shearing
of
,
any affine squashing, stretching, or shearing
of 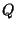 results in a new polyhedron that equally well
satisfies the definition of dual of
results in a new polyhedron that equally well
satisfies the definition of dual of 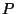 .
More exotic deformations of
.
More exotic deformations of
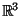 result in a wide range
of possible duals for any particular polyhedron.
result in a wide range
of possible duals for any particular polyhedron.
So such a program or presentation
has a choice to make: which dual to present,
for a given primal polyhedron 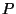 ?
?
First, note that it is not obvious that every polyhedron
has a dual polyhedron at all. We will henceforth restrict our attention
to convex polyhedra: for this class of polyhedra,
we can use the process of reciprocation about a sphere
(which we will define in Section 2 [XXX get xref right])
to produce a dual polyhedron 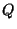 ;
furthermore, reciprocating
;
furthermore, reciprocating 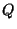 about the same sphere
yields
about the same sphere
yields 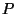 again.
again.
However, the process of reciprocation still leaves some freedom:
it requires a choice of reciprocation center
(which can be any point in the interior of 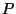 )
and reciprocation radius.
The radius is not particularly problematic: for a given reciprocation center,
changing the reciprocation radius
simply results in a larger or smaller reciprocal polyhedron
)
and reciprocation radius.
The radius is not particularly problematic: for a given reciprocation center,
changing the reciprocation radius
simply results in a larger or smaller reciprocal polyhedron 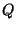 ,
without changing its shape or orientation.
So a reasonable choice for radius might be one that equalizes some measure
of the sizes of
,
without changing its shape or orientation.
So a reasonable choice for radius might be one that equalizes some measure
of the sizes of 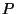 and
and 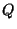 ,
say, their volumes, surface areas, or average
distances from the reciprocation center (measured in any of various ways).
,
say, their volumes, surface areas, or average
distances from the reciprocation center (measured in any of various ways).
The choice of reciprocation center, on the other hand,
is surprisingly problematic.
Since the duality relation is symmetric,
it seems reasonable and desirable
to try to make our canonical-dual-choosing process
symmetric as well.
But obvious choices of reciprocation center violate this desired symmetry.
For example, let's look at what happens when we try
using the centroid (center of mass)
of the primal polyhedron as the reciprocation center.
Starting with 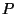 , we find its centroid
, we find its centroid
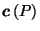 and reciprocate about a sphere centered at
and reciprocate about a sphere centered at
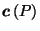 to get the reciprocal polyhedron
to get the reciprocal polyhedron 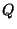 .
Then we find the centroid
.
Then we find the centroid
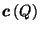 of
of 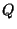 and reciprocate
and reciprocate 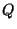 about a sphere centered there to get a polyhedron
about a sphere centered there to get a polyhedron
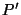 .
.
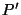 has the same structure as
has the same structure as 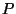 (since they are both dual to
(since they are both dual to 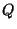 ,
which specifies their structure),
but in general they will
not have the same shape, unless
,
which specifies their structure),
but in general they will
not have the same shape, unless
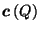 happens to equal
happens to equal
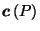 , which is not true in general.
Various other naïve attempts result in exactly the same problem,
and one becomes tempted to believe that no well-behaved center-choosing
strategy exists.
, which is not true in general.
Various other naïve attempts result in exactly the same problem,
and one becomes tempted to believe that no well-behaved center-choosing
strategy exists.
Note that in the special case when 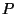 has a center of symmetry
has a center of symmetry 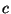 (i.e. a unique point that is fixed by all symmetries of
(i.e. a unique point that is fixed by all symmetries of 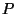 ),
then there is no issue:
),
then there is no issue: 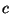 is the natural choice,
and in fact it is the only possible choice,
assuming we want behavior independent of the orientation of
is the natural choice,
and in fact it is the only possible choice,
assuming we want behavior independent of the orientation of 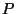 .
This is the case for the regular (Platonic)
and uniform (Archimedian) polyhedra.
So the difficulty arises when we start looking at more general polyhedra
without centers of symmetry,
e.g. certain of the Johnson solids (convex polyhedra whose faces
are regular polygons) [XXX ref].
.
This is the case for the regular (Platonic)
and uniform (Archimedian) polyhedra.
So the difficulty arises when we start looking at more general polyhedra
without centers of symmetry,
e.g. certain of the Johnson solids (convex polyhedra whose faces
are regular polygons) [XXX ref].
Our task is to find a canonical reciprocation center function:
that is, a function assigning to each convex polyhedron a
point in its interior suitable for use as a reciprocation center.
In particular, it must satisfy the desired symmetric behavior described above,
as well as a reasonable continuity condition- continuous changes in 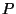 must not result in jumps of the reciprocation center!
At this point, it is not obvious that any such function exists.
must not result in jumps of the reciprocation center!
At this point, it is not obvious that any such function exists.
In this paper, will construct such a function.
[XXX should mention that the function has even better/stronger continuity
than might be expected: it does not jump even if the topology of the polyhedron
changes, e.g. when a face is subdivided by addition of a new edge.]
The construction and proof works not just for convex polyhedra,
but for all compact (i.e. closed and bounded) convex subsets of
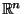
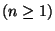 with non-empty interior.
So we start with the following definitions.
with non-empty interior.
So we start with the following definitions.
Definitions:
For 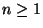 , let
, let
where
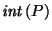 denotes the interior of
denotes the interior of 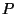 .
.
Definitions:
If
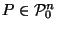 ,
we define the reciprocal
,
we define the reciprocal 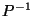 of
of 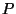 about the unit hypersphere as:
about the unit hypersphere as:
[ XXX warn not to call it ``inverse'' or you will be spanked ]
It easily follows from the definition that reciprocation reverses scale;
that is, for 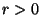 :
:
where
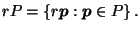
It is also straightforward to check that 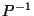 is compact and convex, and contains
is compact and convex, and contains 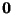 in its interior;
i.e.
in its interior;
i.e.
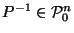 and so
and so
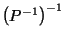 is defined.
is defined.
Proof of Lemma 2.1:
For all
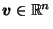 , let
, let
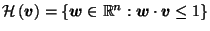 .
Note that
.
Note that
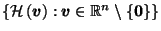 is precisely
the set of closed half-spaces containing the origin in their interiors,
and
is precisely
the set of closed half-spaces containing the origin in their interiors,
and
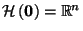 .
Note also the following duality correspondence:
for all
.
Note also the following duality correspondence:
for all
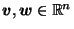 ,
,
Then, given
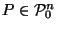 ,
,
On the other hand,
Combining these two ways of looking at reciprocation, we get:
the last equality holding since
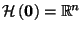 does not affect the intersection.
In other words,
does not affect the intersection.
In other words,
So
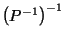 is the intersection of all closed half-spaces
that contain
is the intersection of all closed half-spaces
that contain 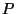 ; that is,
; that is,
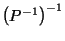 is the closure of the convex hull of
is the closure of the convex hull of 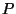 .
But
.
But 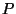 is already convex and closed, so
is already convex and closed, so
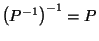 .
.

The proof of Lemma 2.1 used the generally useful fact
that 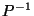 can be thought of in two ways:
either as
the intersection of all closed halfspaces
can be thought of in two ways:
either as
the intersection of all closed halfspaces
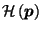 corresponding to points
corresponding to points
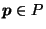 ,
or as
the set of all points
,
or as
the set of all points 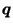 corresponding to the closed halfspaces
corresponding to the closed halfspaces
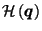 containing
containing 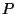 .
Boundary points of
.
Boundary points of 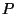 correspond to bounding planes of
correspond to bounding planes of 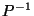 and vice-versa.
In particular, if
and vice-versa.
In particular, if 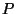 is a polygon or polyhedron,
then so is
is a polygon or polyhedron,
then so is 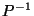 ,
and the vertices of
,
and the vertices of 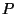 correspond to the sides or faces of
correspond to the sides or faces of 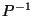 and vice-versa.
and vice-versa.
We now generalize the definition of reciprocation about the unit hypersphere
to that of reciprocation about an arbitrarily sized hypersphere
centered anywhere in the interior of 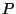 (
(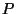 may or may not contain the origin), as follows.
To reciprocate about a hypersphere,
given the hypersphere's center
may or may not contain the origin), as follows.
To reciprocate about a hypersphere,
given the hypersphere's center
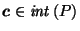 and radius
and radius 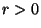 ,
we translate and scale
,
we translate and scale
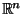 so that the hypersphere has center
so that the hypersphere has center 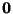 and radius
and radius 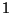 ,
reciprocate, and then apply the inverse scale and translation.
Writing this out and applying (1), we get,
for all
,
reciprocate, and then apply the inverse scale and translation.
Writing this out and applying (1), we get,
for all
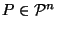 ,
,
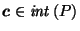 , and
, and 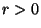 :
:
Then of course
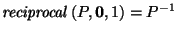 .
[Pictures of reciprocals needed! This paper is self-contained so should try to be helpful to people unfamiliar with reciprocals!]
.
[Pictures of reciprocals needed! This paper is self-contained so should try to be helpful to people unfamiliar with reciprocals!]
Definition:
If
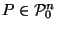 and
and
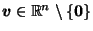 ,
let
,
let
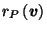 denote the (positive) distance from the origin to the
boundary of
denote the (positive) distance from the origin to the
boundary of 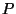 in the direction of
in the direction of 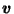 .
.
Proof of Lemma 2.2:
If
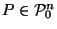 and
and
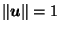 , then
, then
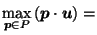 |
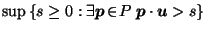 |
|
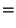 |
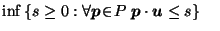 since since 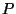 is connected, is connected, |
|
| |
 bounded, and contains bounded, and contains  |
|
 |
 |
|
 |
 |
|
 |
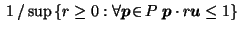 |
|
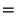 |
 by definition of by definition of  |
|
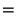 |
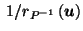 |
|
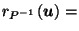 |
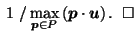 |
|
[XXX make corollary numbers in same sequence as lemma numbers!]
Proof of Corollary 2.1:
Use
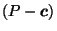 for the
for the 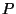 of Lemma 2.2.
of Lemma 2.2.

Definition:
Define
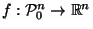 by:
by:
the integral being taken over the (hyper-) area
as 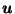 ranges over the unit hypersphere
ranges over the unit hypersphere
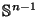 in
in
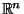 .
.
Intuitively,
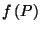 is the weighted average
of all unit vectors, with each weight being equal to
the logarithm (possibly negative) of the distance from the origin
to the boundary of
is the weighted average
of all unit vectors, with each weight being equal to
the logarithm (possibly negative) of the distance from the origin
to the boundary of 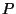 in that direction.
in that direction.
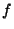 can be thought of as a vector-valued measure of the ``offcenteredness''
of
can be thought of as a vector-valued measure of the ``offcenteredness''
of 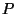 from the origin. In particular, note that when only one part
of the boundary of
from the origin. In particular, note that when only one part
of the boundary of 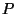 is very close to the origin,
is very close to the origin,
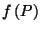 will be weighted heavily in the opposite direction
due to the dominance
of the negative logarithm in the direction of the boundary.
will be weighted heavily in the opposite direction
due to the dominance
of the negative logarithm in the direction of the boundary.
[ XXX mention that the log can be with respect to any base; changing the base multiplies 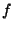 by a scalar,
and all the results of this paper still hold, and the final
reciprocation center is the same ]
by a scalar,
and all the results of this paper still hold, and the final
reciprocation center is the same ]
A somewhat surprising property of
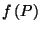 is that it is impervious to
scaling of
is that it is impervious to
scaling of 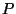 , as the next Lemma shows.
, as the next Lemma shows.
Proof of Lemma 3.1:
At this point, we remark that in our quest to produce a canonical reciprocation
center, a reasonable approach might be to look for a (hopefully unique)
point
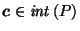 such that
such that
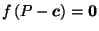 ,
and hope that when
we do the same
to the reciprocal of
,
and hope that when
we do the same
to the reciprocal of 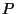 with respect to a sphere centered at
with respect to a sphere centered at 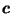 ,
the result is the same point
,
the result is the same point 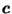 .
Lemma 3.1 shows that the radius of reciprocation is irrelevant;
that is, if this works for some radius than it will work for all radii.
.
Lemma 3.1 shows that the radius of reciprocation is irrelevant;
that is, if this works for some radius than it will work for all radii.
Unfortunately, it turns out that it does not work, since
it can be (and often is) that
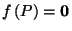 and
and
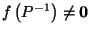 .
However, we will now use
.
However, we will now use  to construct a similar function
to construct a similar function  that does not suffer from this problem.
that does not suffer from this problem.
Definition:
Define
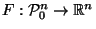 by:
by:
The next Lemma shows that the analogue of Lemma 3.1 holds for 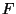 instead of
instead of 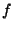 .
.
Proof of Lemma 3.2:
Proof of Lemma 3.3:
Now we would like to show that
for all
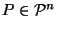 ,
there is a unique
,
there is a unique
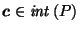 such that
such that
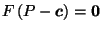 .
This will be established by the next two Lemmas.
.
This will be established by the next two Lemmas.
Definition:
For
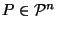 ,
define
,
define
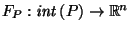 by:
by:
[XXX I think this proof would look less cluttered if c wasn't throughout it. So,
should argue for when c = 0 and then generalize (perhaps as a corollary).
Note this is fine for the refs to (8) and (10) later in Lemma 3.5 since they only use the c=0 case. ]
Proof of Lemma 3.4:
Given
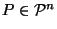 ,
,
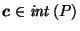 ,
,
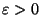 ,
and
,
and
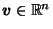 such
such
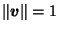 and
and
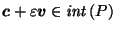 ,
we must show that
,
we must show that
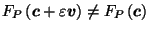 .
We will do this by showing that
.
We will do this by showing that
By definition of  and
and 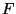 ,
,
We want to show this is 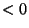 ,
so it suffices to show that
,
so it suffices to show that
and
Proof of (8):
Define
For each
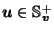 , let
, let
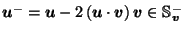 ;
i.e.
;
i.e. 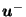 is
is 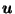 with its ``
with its ``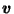 '' component reversed.
Note that
'' component reversed.
Note that
Since the disjoint union
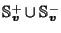 is all of
is all of
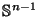 except for a set of area zero,
we can pair up the terms in the definition of
except for a set of area zero,
we can pair up the terms in the definition of
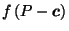 ,
as follows:
,
as follows:
So
Using this and the analogous expression for
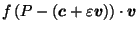 , we get:
, we get:
To show that this is 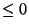 , it suffices to show that the
integrand is
, it suffices to show that the
integrand is 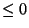 for all
for all
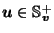 .
Each
.
Each
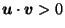 by definition of
by definition of
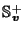 ,
so we just need to show that
,
so we just need to show that
i.e. that
i.e. that
Figure 1:
Slice of 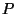 showing that
showing that
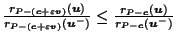 .
.
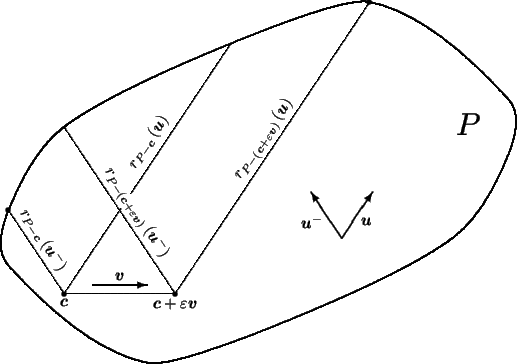 |
Figure 1 shows
the intersection of 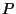 with a 2-d plane containing
with a 2-d plane containing
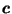 ,
,
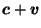 , and
, and
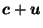 .
The fact that
.
The fact that
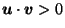 guarantees that the two outer lines,
from
guarantees that the two outer lines,
from 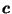 to
to
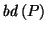 in the direction of
in the direction of 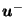 and from
and from
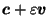 to
to
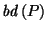 in the direction of
in the direction of 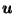 ,
do not cross.
The two inner lines may or may not cross.
If the part of the boundary of
,
do not cross.
The two inner lines may or may not cross.
If the part of the boundary of 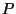 leading from
leading from
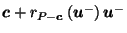 to
to
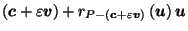 is a straight line,
then by similar triangles (14) holds as equality;
otherwise the denominator of the LHS and the numerator of the RHS
(i.e. the lengths of the inner slanted lines in Figure 1)
both become bigger, and so (14) still holds.
is a straight line,
then by similar triangles (14) holds as equality;
otherwise the denominator of the LHS and the numerator of the RHS
(i.e. the lengths of the inner slanted lines in Figure 1)
both become bigger, and so (14) still holds.
Proof of (10):
We want to show that this integral is 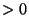 .
When
.
When
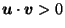 , the (positive) denominator in (15) is
, the (positive) denominator in (15) is 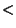 the
(positive) numerator, so the logarithm is
the
(positive) numerator, so the logarithm is 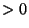 and so the integrand is
and so the integrand is 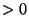 .
Similarly, when
.
Similarly, when
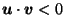 , the logarithm is
, the logarithm is 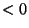 and so again the integrand is
and so again the integrand is 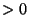 .
So the integrand of (15) is
.
So the integrand of (15) is 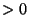 for all
for all 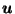 for which
for which
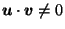 ,
which is all of
,
which is all of
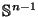 except for a set of area zero;
therefore the integral is
except for a set of area zero;
therefore the integral is 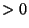 , as desired, and so (10) is established.
This completes the proof of Lemma 3.4.
, as desired, and so (10) is established.
This completes the proof of Lemma 3.4.

Proof of Lemma 3.5:
We can assume without loss of generality that the interior
of 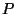 contains the origin
(otherwise pick an arbitrary interior point of
contains the origin
(otherwise pick an arbitrary interior point of 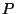 and call it the origin);
so
and call it the origin);
so
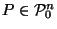 .
It seems clear that as
.
It seems clear that as
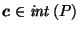 approaches the boundary
approaches the boundary
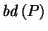 ,
,
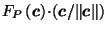 will decrease rapidly.
So our strategy is to find
will decrease rapidly.
So our strategy is to find
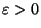 small enough so that
for all
small enough so that
for all
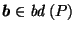 ,
for all
,
for all 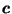 on the segment strictly between
on the segment strictly between
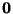 and
and 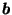 with
with
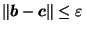 ,
,
then we will be able to apply Lemma A.2 (see Appendix)
using the function 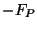 on a slightly shrunken
on a slightly shrunken 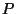 ,
with the amount of shrinkage based on
,
with the amount of shrinkage based on
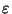 .
.
We will need to do some calculations
in order to see how small we need to make
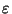 .
.
Let
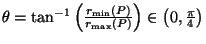 ,
where
,
where
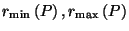 are respectively
the min and max distances from the origin to
are respectively
the min and max distances from the origin to
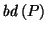 .
.
For all
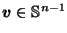 , define
, define
That is,
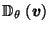 is
the closed (hyper-) spherical
disk of radius
is
the closed (hyper-) spherical
disk of radius 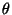 centered at
centered at 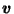 .
.
Figure 2:
Pie and ice cream.
![\begin{figure}\begin{center}
\setlength{\unitlength}{\textwidth / 22}%% (use ca...
...akebox(0,0)[b]{$\vec{v}$}}
\par\thinlines\end{picture} \end{center} \end{figure}](img367.gif) |
Let 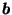 be an arbitrary boundary point of P,
and
be an arbitrary boundary point of P,
and 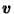 =
=
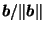 , so
, so 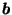 =
=
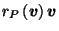 .
.
Note that
for all
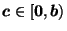 ,
for all
,
for all
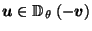 ,
,
This can be seen geometrically (see Figure 2)
since, for such 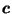 ,
the pie-slice-shaped set
,
the pie-slice-shaped set
is a subset of the ice-cream-cone-shaped convex hull of
which is a subset of 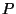 .
(
.
(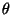 was chosen to be small enough so that this would work for all
was chosen to be small enough so that this would work for all 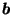 on the boundary of
on the boundary of 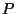 ).
).
For each
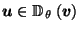 , define
, define
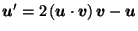 ;
i.e.
;
i.e. 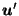 is
is 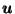 reflected across
reflected across 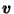 . Then
. Then
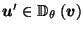 , and
, and
Define
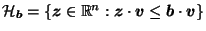 .
.
Then for any 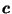 strictly between
strictly between 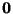 and
and 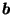 ,
,
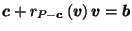 is on the boundary
of the closed halfspace
is on the boundary
of the closed halfspace
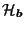 ,
so by convexity of
,
so by convexity of 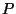 ,
for each
,
for each
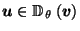 , at least one of
, at least one of 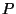 's boundary points
's boundary points
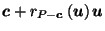 and
and
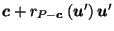 is in
is in
 .
[XXX picture would be nice]
I.e.
.
[XXX picture would be nice]
I.e.
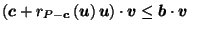 or or 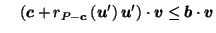 |
|
i.e.
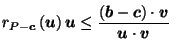 or or 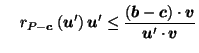 |
|
(since
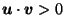 and
and
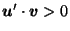 ,
since
,
since
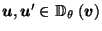 ).
I.e., by (17),
).
I.e., by (17),
But for
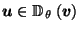 , we know that
, we know that
so, since the cosine function is decreasing on the interval
![$ \left[0,{\pi}/{4}\right]$](img420.gif) ,
,
Applying this to (18), we get,
for
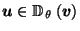 :
:
Let's look at the contributions
the disjoint sets
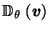 ,
,
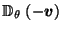 ,
and
,
and
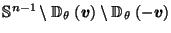 make to
make to
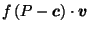 when
when
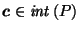 lies on the segment
lies on the segment
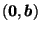 and
and
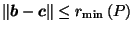 .
.
[XXX In all three of the following computations, I think we can avoid
the
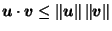 step, so that we end up with a bunch of integrals of
step, so that we end up with a bunch of integrals of
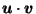 in (24) so that it becomes more uniform as well as a tighter
bound. If we care.]
in (24) so that it becomes more uniform as well as a tighter
bound. If we care.]
For such 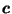 ,
the contribution that
,
the contribution that
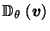 makes to
makes to
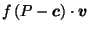 is:
is:
| |
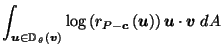 |
|
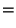 |
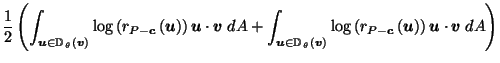 |
|
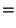 |
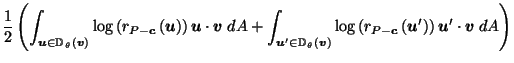 |
|
 |
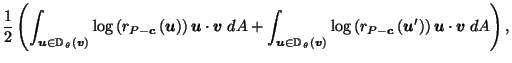 |
|
| |
 since since
 and and
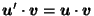 |
|
 |
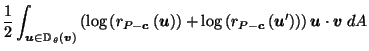 |
|
 |
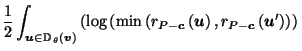 |
|
 |
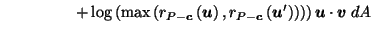 |
|
| |
[XXX separate next step into two steps. Also I think maybe
 can be replaced with can be replaced with
 ] ] |
|
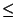 |
 by (19) and by (19) and
 |
|
 |
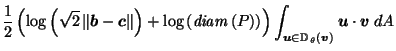 |
|
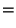 |
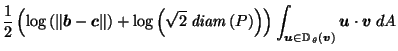 |
|
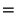 |
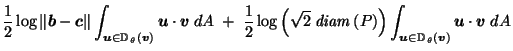 |
|
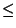 |
 |
|
 |
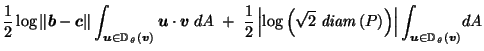 |
|
| |
 since since
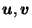 are unit vectors are unit vectors |
|
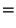 |
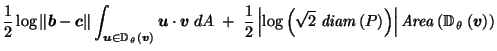 |
(15) |
where
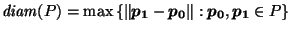 exists and is finite by compactness of P.
exists and is finite by compactness of P.
The contribution that
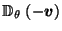 makes to
makes to
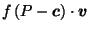 is:
is:
| |
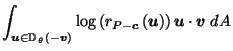 |
|
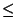 |
 by (16) and by (16) and
 |
|
 |
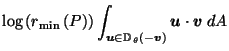 |
|
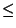 |
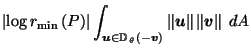 |
|
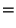 |
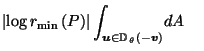 since since
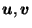 are unit vectors are unit vectors |
|
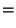 |
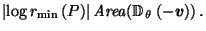 |
(16) |
And the contribution that
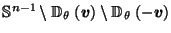 makes to
makes to
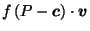 is:
is:
by the same pairing argument as the proof of (8) in Lemma 3.4, since 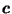 is in direction
is in direction 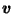 from
from 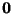
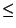 |
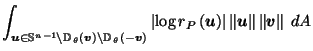 |
|
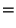 |
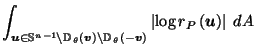 since since  are unit vectors are unit vectors |
|
 |
 |
|
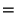 |
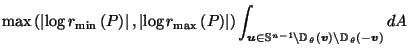 |
|
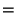 |
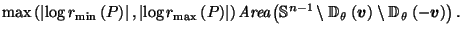 |
(17) |
Putting it all together, we get:
| |
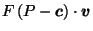 |
|
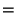 |
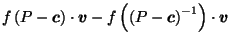 by definition of by definition of 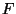 |
|
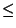 |
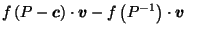 by (10) in proof of Lemma 3.4, by (10) in proof of Lemma 3.4, |
|
| |
 since since  is in direction is in direction  from from 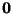 |
|
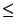 |
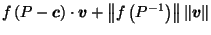 |
|
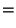 |
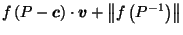 |
|
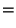 |
 by definition of by definition of 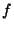 |
|
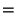 |
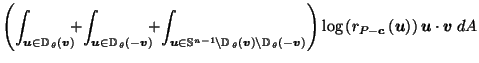 |
|
| |
 |
|
 |
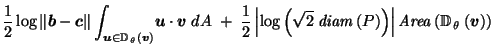 |
|
| |
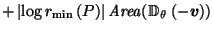 |
|
| |
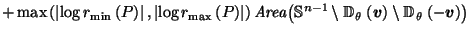 |
|
| |
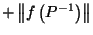 |
(18) |
by (20),
(21),
and (23).
Notice that neither the integral nor the areas appearing in (24)
depend on 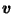 at all;
they are the same for all
at all;
they are the same for all 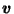 ,
depending only on
,
depending only on 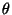 which is a constant (depending on
which is a constant (depending on 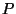 ).
So the only part of (24) that is not constant
is
).
So the only part of (24) that is not constant
is
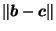 ,
and so we can rewrite (24) as:
,
and so we can rewrite (24) as:
for appropriate constants  ,
,  (depending on
(depending on  ).
Note that
).
Note that 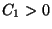 ,
so we can make the RHS of (25)
less than any desired target by choosing sufficiently small
,
so we can make the RHS of (25)
less than any desired target by choosing sufficiently small
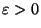 and requiring
and requiring
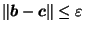 ;
then the LHS
;
then the LHS
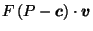 will be less than the desired target as well.
will be less than the desired target as well.
Now we are finally ready to show that
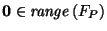 .
By the previous paragraph (setting our ``desired target'' to be 0), choose
.
By the previous paragraph (setting our ``desired target'' to be 0), choose
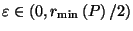 small enough so that for all
small enough so that for all
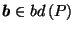 and
and 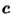 strictly between
strictly between 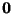 and
and 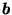 with
with
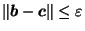 ,
,
where
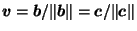 ; i.e.
; i.e.
Define
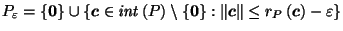 ; i.e.
; i.e.
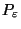 is
is 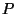 with its boundary shrunk by
with its boundary shrunk by
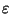 units radially towards the origin.
Then
units radially towards the origin.
Then
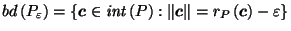 ,
so all points
,
so all points
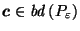 satisfy (27).
satisfy (27).
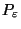 is not necessarily in
is not necessarily in
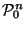 since it typically
is not convex[XXX picture might be nice]; however its convex hull
since it typically
is not convex[XXX picture might be nice]; however its convex hull
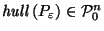 ,
and
,
and
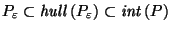 (the latter inclusion being since
(the latter inclusion being since
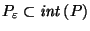 and
and
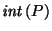 is convex).
Then
is convex).
Then
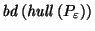 is even closer to
is even closer to
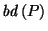 than
than
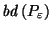 is,
so all points
is,
so all points
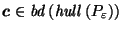 satisfy (27) as well.
So the function
satisfy (27) as well.
So the function 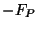 restricted to
restricted to
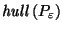 satisfies the hypotheses of Lemma A.2 (see Appendix),
so by that Lemma there exists
satisfies the hypotheses of Lemma A.2 (see Appendix),
so by that Lemma there exists
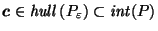 such that
such that
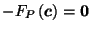 ,
and so
,
and so
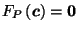 .
.

Exercise 1
If
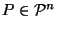
,
show that
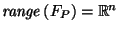
.
Definition:
If
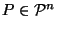 , define
, define
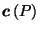 to be the unique point
to be the unique point
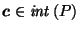 such that
such that
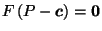 ;
i.e. such that
;
i.e. such that
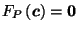 .
Existence and uniqueness of
.
Existence and uniqueness of
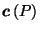 is guaranteed by Lemmas 3.5 and 3.4
respectively.
is guaranteed by Lemmas 3.5 and 3.4
respectively.
Theorem 1
If
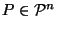
and
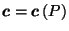
,
then for any
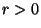
,
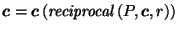
.
[ XXX in other words,
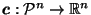 is a canonical reciprocation function,
if we define that earlier]
is a canonical reciprocation function,
if we define that earlier]
Proof of Theorem 1:
Assuming
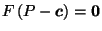 ,
we must show
,
we must show
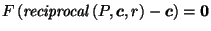 .
.
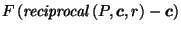 |
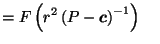 by (7) by (7) |
|
| |
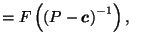 by Lemma 3.2 by Lemma 3.2 |
|
| |
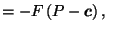 by Lemma 3.3 by Lemma 3.3 |
|
| |
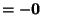 by assumption by assumption |
|
| |
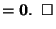 |
|
[ XXX mention possible choices and relationships with the choice of canonical center ]
[ XXX closed formula? algorithm? ]
[ XXX other similar log-based definitions I've thought of and haven't disproved?]
[ XXX other definitions based on matching the primal and dual CG, for some notion of CG? ]
[ XXX a definition that is the centroid when P is a triangle? (or simplex)]
[ XXX characterize all canonical-reciprocation-center functions. what does the space of all such functions look like? Does it have isolated points? ]
[ XXX algebra of them? e.g. can we linearly interpolate between any two of them? ]
[ XXX write me]
This appendix proves two topological lemmas related to Brower's fixed-point
theorem.
Lemma A.2 was used in the proof of Lemma 3.5.
Definitions:
For 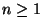 , let
, let
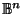 be the closed unit ball in
be the closed unit ball in
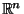 ,
and let
,
and let
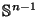 be its boundary.
That is,
be its boundary.
That is,
Lemma A.1
If
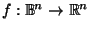
is continuous
and
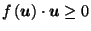
for all
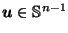
,
then
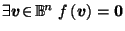
.
Proof of Lemma A.1:
Assume, to the contrary, that the origin is not in the range of 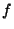 .
Then we can define a continuous function
.
Then we can define a continuous function
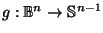 by:
by:
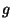 is a continuous mapping from
is a continuous mapping from
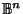 to
to
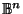 .
Brower's fixed point theorem states that any such mapping
must have a fixed point, so there exists
.
Brower's fixed point theorem states that any such mapping
must have a fixed point, so there exists
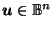 such that
such that
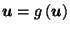 (and so
(and so
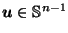 ).
So
).
So
But then
which contradicts the assumption that
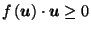 for all
for all
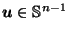 .
.

Lemma A.2
If
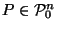
(that is,
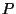
is a compact convex subset of
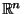
containing
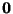
in its interior),
and
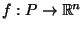
is a continuous function
such that
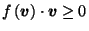
for all
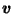
on the boundary of
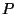
,
then
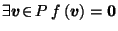
.
Proof of Lemma A.2:
The idea is to simply squash and stretch 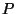 radially from the origin
so that it becomes the unit ball, and then apply Lemma A.1.
Define a homeomorphism
radially from the origin
so that it becomes the unit ball, and then apply Lemma A.1.
Define a homeomorphism
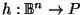 by:
by:
where
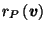 is the distance from the origin to the boundary
of
is the distance from the origin to the boundary
of 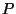 in the direction of
in the direction of 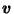 .
Then the composite function
.
Then the composite function
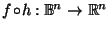 is continuous, and for all
is continuous, and for all
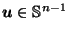 ,
,
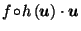 |
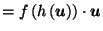 |
|
| |
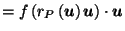 |
|
| |
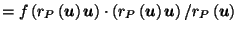 |
|
| |
 since since
 is on the boundary of is on the boundary of  . . |
|
So
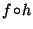 satisfies the conditions
of Lemma A.1,
so the origin is in the range of
satisfies the conditions
of Lemma A.1,
so the origin is in the range of
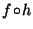 and therefore is in the range of
and therefore is in the range of 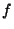 .
.

- 1
- John Conway. Personal communication, September 17 2002.
A Canonical Reciprocation Center
For Convex Objects
This document was generated using the
LaTeX2HTML translator Version 2002 (1.62)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -html_version 3.2 -split 0 -math -image_type gif -transparent -no_reuse -no_navigation CanonicalReciprocationCenter.latex
The translation was initiated by on 2003-07-01
2003-07-01
![]() is the canonical center of
is the canonical center of ![]() ,
and
,
and ![]() is the reciprocal of
is the reciprocal of ![]() with respect to a hypersphere
of any radius centered at
with respect to a hypersphere
of any radius centered at ![]() , then the canonical center
of
, then the canonical center
of ![]() is also
is also ![]() .
.
![]() with non-empty interior.
This function is continuous under continous deformations
of the compact convex set,
and it commutes with rotations, translations, reflections,
and uniform scalings of
with non-empty interior.
This function is continuous under continous deformations
of the compact convex set,
and it commutes with rotations, translations, reflections,
and uniform scalings of
![]() .
This answers a $1000 question posed by
John Conway [1].
.
This answers a $1000 question posed by
John Conway [1].
![]() ''?]
''?]
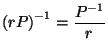
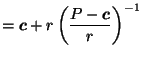
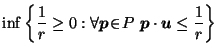
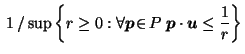
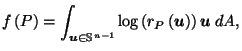
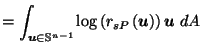
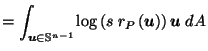
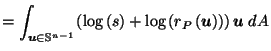
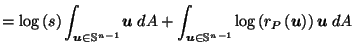
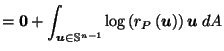
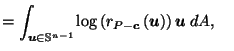 by definition of
by definition of 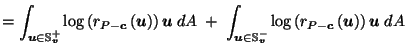
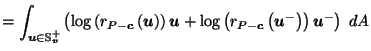
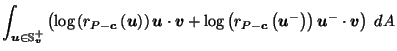
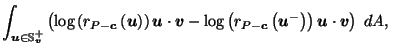 by (
by (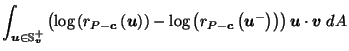
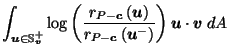
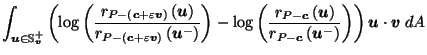
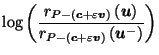
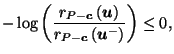
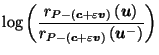
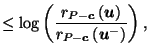
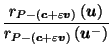
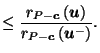

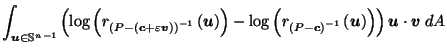
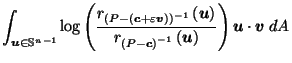
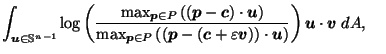 by Corollary
by Corollary 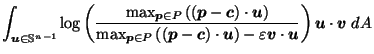
![\begin{figure}\begin{center}
\setlength{\unitlength}{\textwidth / 22}%% (use ca...
...akebox(0,0)[b]{$\vec{v}$}}
\par\thinlines\end{picture} \end{center} \end{figure}](img367.gif)
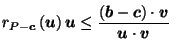 or
or 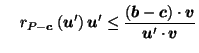
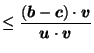
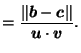
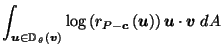
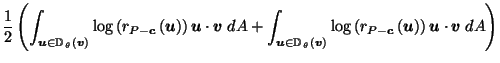
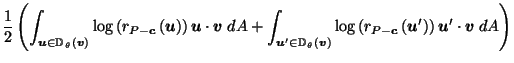
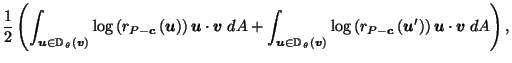
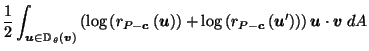
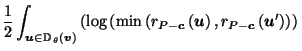
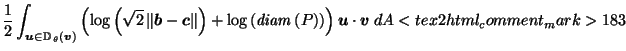 by (
by (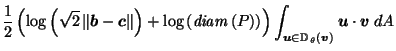
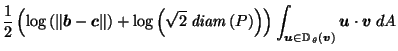
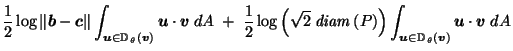
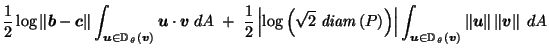
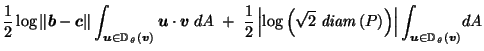
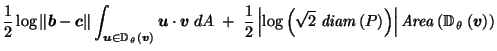
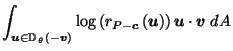
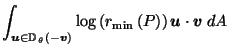 by (
by (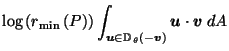
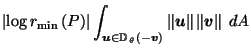
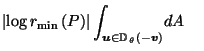 since
since
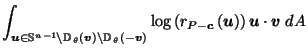
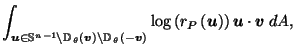
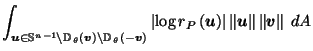
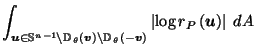 since
since 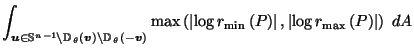
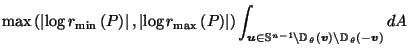
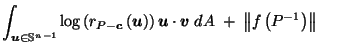 by definition of
by definition of